Tutorial of Unsupervised Feature Learning and Deep Learning by Andrew Ng
Neural Networks
activation function:
- sigmoid function: 值域[0,1]
\begin{equation}
f(z) = \frac{1}{1+\exp(-z)}
\end{equation}
一阶导数为:$f’(z) = f(z)(1-f(z))$
- tanh function (hyperbolic tangent) 双曲正切函数: 值域[ − 1,1]
\begin{equation}
f(z) = \tanh(z)=\frac{e^z-e^{-z}}{e^z+e^{-z}}
\end{equation}
一阶导数为:$f’(z) = 1-(f(z))^2$
Neural Network model
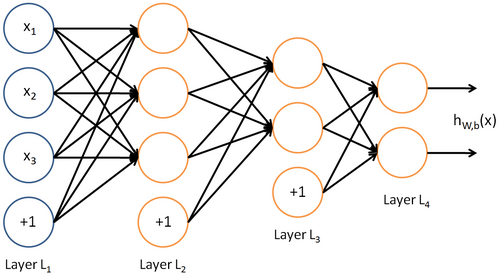
input layer $\to$ hidden layer $\to$ output layer
每层的神经元数量不计bias unit(bias unit对应intercept term,y=Wx+b 中的b)
设神经网络有$n_l$层,则图中 input layer (记为$L_1$,3 input units) $\to$ hidden layer ($L_2$,3 hidden units; $L_3$,2 hidden units) $\to$ output layer (记为$L_{n_l}$,2 output units)
第$l$ 层对应的参数为$W^l,b^l$,则
\begin{equation}
z^{l+1} = W^l a^l+b^l
\end{equation}
\begin{equation}
a^{l+1} = f(z^{l+1})
\end{equation}
$a^{l+1}$是一个向量,代表第$l+1$层的activation。其中$a^1$是输入x,$a^{n_l}$为输出y
feedforward neural network, the connectivity graph does not have any directed loops or cycles
Backpropagation Algorithm
反向传播算法从输出层开始,反向计算每个节点的残差,并用这些残差计算代价方程对每一个参数的偏导数。